Graph

无向图

表示

alt

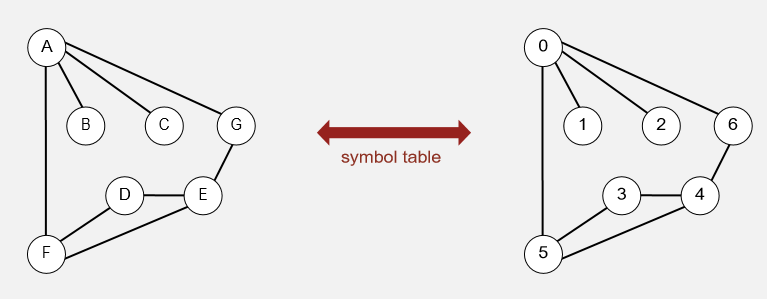
通过符号表，将名称转换成序号，达到通用图表示的目的

问题

路径：

  • s和t之间是否可达路径（DFS，BFS）
  • s和t之间的最短路径（BFS）

环路：

  • 图中是否存在环路
  • 是否存在一个环路经过图上所有点并且只路过一次
  • 是否存在一个环路经过图上所有边并且只路过一次

连接：

  • 图上所有点是否可以全部连接在一起（DFS，BFS）
  • 最佳的方法是什么？最小生成树
  • 是否能够删除一个点将图一分为二？割点

平面度：

  • 是否可以不跨边画出同构图？
  • 两个邻接列表是否可以表示同一个图？

邻接矩阵

alt

采用二维bool数组，表示i和j之间是否存在边

邻接表

alt

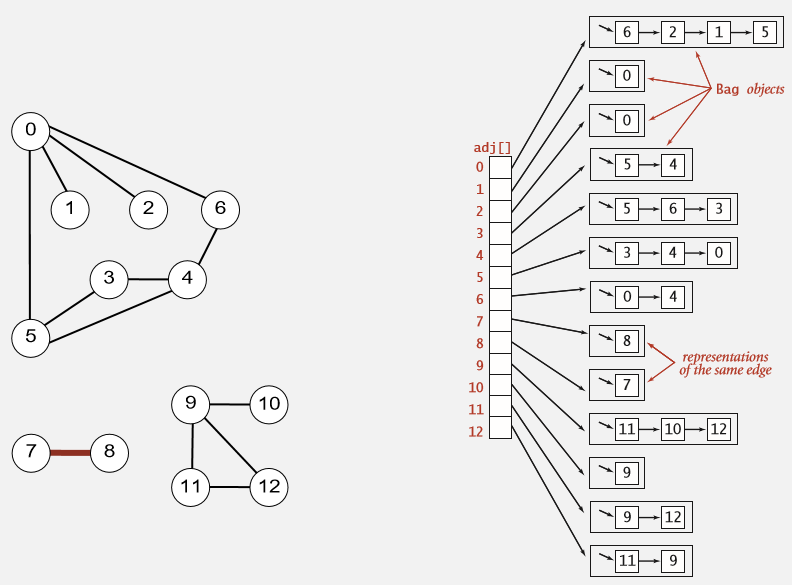
采用二维list数组，表示i和i所有边的对应关系

class Graph:
    def __init__(self, v):
        self.v = v
        self.e = 0
        self.adj = [[] for i in range(v)]

    def get_v(self):
        return self.v

    def get_e(self):
        return self.e

    def __validate_v(self, v):
        if v < 0 or v >= self.v:
            raise Exception("{} illegal".format(v))

    def add_edge(self, v, w):
        self.__validate_v(v)
        self.__validate_v(w)
        self.e += 1
        self.adj[v].append(w)
        self.adj[w].append(v)

    def get_adj(self, v):
        self.__validate_v(v)
        return self.adj[v]

    def get_degree(self, v):
        self.__validate_v(v)
        return len(self.adj[v])

    def __str__(self):
        return "v:" + str(self.v) + " e:" + str(self.e) + " adj: " + str(self.adj)



if __name__ == '__main__':
    g = Graph(7)
    g.add_edge(0, 1)
    g.add_edge(0, 2)
    g.add_edge(0, 5)
    g.add_edge(0, 6)
    g.add_edge(3, 4)
    g.add_edge(3, 5)
    g.add_edge(4, 5)
    g.add_edge(4, 6)

    print(g)